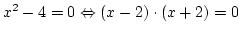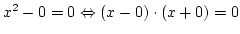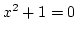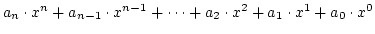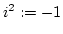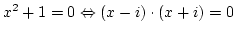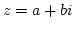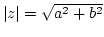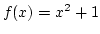2001, das Hoffnungs- oder Horrorjahr so mancher Science-Fiction Phanstasie, was hat es unter neuer Führung dem Verein gebracht? In erster Linie einen sehr erfreulichen Neuzugang: Herr Prof. Dolge ist nun noch einmal offiziell im Verein zu begrüßen.

Dann natürlich die Soundaustellung, nach einjähriger Pause wieder in der Steinhalle in Emmendingen, bei der sich alle aktiv beteiligten, was ich höchst erfreulich und bemerkenswert fand. Denn die meisten Mitglieder - mich eingeschlossen - bedurften bisher einer gewissen Eingewöhnungsphase, bis sie selbst als Produzenten aktiv wurden.

Elektronische Musik steht auch weiterhin im Spannungsfeld zwischen Musik, Naturwissenschaft, Mathematik und Technik, die Auseinandersetzung damit berührt in gewisser Weise sogar philosophische Fragestellungen, was auch an dieser ZeM-Heft Ausgabe deutlich wird.

Da dieses Heft zum Jahresende fertig werden wird, wünsche ich allen Mitgliedern ein gutes und künstlerisch befriedigendes Jahr 2002.

Rettbehr Meier

 

Seit ca. 20 Jahren haben wir, besser: hat man die Möglichkeit, besser: die Möglichkeiten, elektronische, besser: elektroakustische Musik, besser: Sounds herzustellen, besser: sie zu produzieren, schlechter: zu komponieren. Schon bis hier eine Menge neuer sprachlicher Ausdrücke, die eigentlich einer genauen Definition, also einer erforderlichen Eingrenzung harren. So ist wohl die Bestimmung "elektroakustisch" gar nicht so unzutreffend, denn das Wort elektro- elektronisch ist zu weitläufig. Wir wollen und müssen den Bezug zum Hören herstellen und das dazugehörige Wort ist griechisch akouein = hören. Lassen wir die anderen Worte auf sich beruhen, dass aber Musik durch Klang und Komposition durch Produktion ersetzt werden, wird hier behauptet, zunächst ohne Begründungen und Beweise zu liefern.

Eine kurze Gegenüberstellung: elektronische (gleich elektroakustische) Klänge sind möglich, potentiell, klassische Musik ist tatsächlich, real. Elektronische Musik ist stets neu zu erzeugen und zugleich erzeugbar, klassische Musik ist als schon immer gegeben erstarrt. Elektronische Musik ist flüssig wie Wasser und Wolken, sich stets verändernd, flüchtig, kurz: sie ist frei und offen. Klassische Musik ist gebunden, Gefolgschaft fordernd, die Freiheit einschränkende Bedingungen stellend u. v. m.

Man hört und sieht schon (man sieht keine Musiker): Offenbar besteht ein grundlegender Unterschied zwischen dem elektronischen Sound und der klassischen Musik der Töne. Tatsächlich, damit ist alles gesagt in vordergründiger, kurzer Theorie und einfach ausgedrückt. Hier ist offensichtlich ein Bruch passiert, so wie es viele dieser Symmetriebrüche in dieser Welt gibt: so z. B. die Spaltung anorganisch - organisch. Dieser Bruch vom Organischen: "Musik aus dem Bauch", "Musik, die zu Herzen geht" zum Anorganischen: "technisch, tot, maschinell, intellektuell" muss gehört und gesehen ("Lautsprecher") werden, um Zugang zu finden zu diesem anorganischen und sicher inhumanen Sound.

Wir haben in den letzten 20 Jahren solche unorganischen Klänge "vorgeführt", daraus entstand der so unbefriedigende Ausdruck "Vorführung". Dennoch: Vielleicht war das Wort gar nicht so abwegig, wir führten "vor" und nicht "nach", wir spielten nicht "nach", sondern "vor", wir gingen nach vorn in eine Zukunft, die damals, quasi aus dem Nichts entstand, mit Synthies, Recordern und Keyboardboxen hin zu dem, was heute nach 20 Jahren im Mittelpunkt der Soundelektronik steht. Mag sein, dass wir damit ein vorläufiges Ende erreicht haben, zumindestens so lange noch Klang über technische Medien als Ausgabe und Ohren als Empfänger in Geltung sind.

Noch einige Reflexionen zu den Begriffspaaren Komposition - Produktion oder Plan - Ablauf oder wieder: Mögliches - Gemachtes oder Vorgegebenes - Gefestigtes. Ein Reinhören in die "Klingende Steinhalle" dieses Jahres gibt Aufschlüsse und Erkenntnisse. Jeweils zu Beginn der drei Veranstaltungen erklang eine echte, sich produzierende, umfassende Soundvorführung: Cassettenrecorder, ein Mischpult wurden unregelmäßig mit den Reglern bedient, die freie Regel ergab lediglich eine statistische Verteilung der Reglerbewegung. Was die Cassetten an Klangmaterial abgaben, war weitgehend unbekannt: produzierte Klänge aus 20 Jahren mit verschiedenen Instrumenten und Programmen. Das Ergebnis war vielleicht positiv und negativ verblüffend, es war aber eines: unvorherhörbar und nicht mehr reproduzierbar. Sicher: Die Abläufe hätten auf einem modernen HD-Rekorder gespeichert werden können, eine Komposition mit motorgesteuerten Fadern, aber das hätte eines zunichte gemacht: die totale Freiheit und Freizügigkeit der Abläufe. Hätte jemand eine "Aufnahme" machen wollen, hätte man zurufen müssen: "Bitte nicht, das ist zum einmaligen Hören und Vergessen gemacht". Eine kontingente, zufällige Musik und sagen wir ruhig: Musik.

Im Vorraum der Steinhalle erklang eine andere Produktion: Softwareprogramme hatten unter gegebenen Randbedingungen Klänge erzeugt, manche gleich oder ähnlich, leise, meditativ zum Mithören einladend. Diese Abläufe waren nun reproduzierbar gemacht worden, die Freiheit der kontingenten Produktion war hier festgestellt worden, sie sollte nicht vergessen werden, sie sollte Geschichte werden und darum auch einmalig sein.

Die neuen Produktionen können aber auch - und das nicht zu knapp - Anleihen nehmen an klassischen Vorbildern: der fixierten, einmalig in jeder Zeit reproduzierbaren Komposition, Stücke, mit Namen versehen, auf etwas hinweisend, also eine Referenz habend, zeitlich begrenzt. Diese Stücke machen das Hören einfacher, befreit von der lähmenden Ungewissheit, nicht zu wissen, wo man ist und was das ist.

Die "Klingende Steinhalle" wird für die Elektronische Musik selbst zum Symbol. Die Halle ist eigentlich Angebot: mit Menschen gefüllt zu sein, die ausgerichtet auf Redner oder Musiker hingewandt sind, fixiert und geführt mit bedeutenden und aussagekräftigen Medien. Bei uns erklang die Halle mit bedeutenden neuen, bedeutungslosen Klängen, die nicht als musikalische Medien auf anderes hinweisen, etwa auf die "höhere, bessere Welt" oder die Menschen zum gemeinsamen Gebet vereinen, hin zu der Apsis, die auch auf gottesdienstliche Verwendung der Halle hinweist.
Die Halle erklang bei uns in sich als Raum gewordener Klang. Sie erklang, wie wenn sie sagen wollte: "Sono, ergo sum". Es erklingt, also erklingt es. So haben wir vielleicht ohne es zu wollen und zu ahnen einen solchen Quantensprung und auch eine Traditionsverletzung in der "Klingenden Steinhalle" vollzogen. Das will viel heißen: Der Weg von Musik zum Sound, aber auch der Weg vom "ich bin, ich spiele" zu "es spielt" und "es ist". Die "Klingende Steinhalle" klingt, hoffen wir, noch mehrere Jahre.

 

Was ist das Neue? Diese Frage wurde vor kurzer Zeit auf einer Zusammenkunft von Pädagogen gestellt, die sich mit den Neuen Medien etwas intensiver beschäftigen, bezogen auf das Neue an den Neuen Medien. Wir erhielten eine durch wissenschaftliche Literatur gestützte Antwort: Das Neue an den Neuen Medien ist die integrative Verknüpfung der Medien auf digitaler Basis.

Das Funktionieren beruht auf der Navigation und der Rückmeldung (Interaktion). Durch die Neuen Medien, das haben wir alle inzwischen nicht nur gelesen oder gehört, sondern auch selbst erfahren, ändert sich der Umgang mit Wissen, der Erwerb von Informationen, die Art des Lernens, die Arbeitsmethoden und v.a. das Internet, der Inbegriff für Neue Medien, verändert unser Denken und auch unsere Verhaltensweise. Dies wird besonders am Leseverhalten deutlich, wie in folgendem Text von Ernst Fischer, Professor am Institut für Buchwissenschaft an der Johann-Gutenberg-Universität Mainz und Mitglied des Encarta-Beratergremiums, beschrieben: Elektronische Netzwerke sind außerdem ein flüchtiges Medium: "Der User kann sicher sein, immer überwältigend viel an Information anzutreffen, aber niemals kann er sicher sein, die Informationsangebote unverändert wieder so anzutreffen, wie er sie schon einmal gesehen hat. Dieser Flüchtigkeit und der bloßen Virtualität der Kommunikationswelten ist der Mensch aufgrund seiner in prähistorischer Zeit erworbenen Grundausstattung nicht ohne weiteres gewachsen, er muß sich des Dauernden vergewissern, um sein Bewußtseinskontinuum von außen her zu stabilisieren. Die "Antiquiertheit des Menschen" (Günther Anders) angesichts des technologischen Fortschritts wird einmal mehr offenbar. ... Schon sind aber Anpassungsleistungen zu beobachten, durch die sich die geistigen Prozesse selbst verändern. Hypertexte erfordern ein anderes Leseverhalten als der lineare Text des Buches, bei dem es Anfang und Ende und für den Leser jederzeit Gewißheit darüber gibt, an welchem Punkt des Mitteilungskontinuums er sich befindet. Wenn es zutrifft, daß elektronische Netzwerke die Struktur menschlichen Denkens zutreffender abbilden als das Buch, dann wäre in dieser strukturellen Affinität zum assoziativen Denken das Faszinosum des Internet begründet, das als ein "externes Gehirn" betrachtet werden kann. Netzkommunikation tritt uns ähnlich wie Lesen bereits als eine eigene Kulturtechnik entgegen. Das Flanieren in Cybercity fördert ein geistiges Nomadentum, erweitert unser Realitätsverständnis um eine neue mediale Dimension, - der Mensch bleibt aber auch hier das Maß aller Dinge".

Wir von ZeM haben uns nun nicht Multimedia verschrieben, wollen den Sound pur, hören und sonst nichts - aber: trifft nicht das Grundsätzliche des oben festgestellten Sachverhalts auf die Elektronische Musik zu? Kann man hier vielleicht von einem Fraktal sprechen? Und was ist dann damit genau gemeint?

Nehmen wir den einführenden Text "Elektronischer Klang" zu unserer Veranstaltung "Klingende Steinhalle" vom September 2001: Dem linearen Vorgehen beim Lesen eines Buches entspricht die Komposition, die Anfang und Ende hat, deren Ablauf in jedem Teil zeitlich genau festgelegt ist. So wie jedes Kapitel in einem Buch seinen Platz im Kosmos des Buches hat, bilden die Teile einer Komposition ein organisiertes Ganzes. Ein Musikstück aber, dessen Ablauf der Zufall regiert, ein Prozess, nicht komponiert, ermöglicht ein "Flanieren", ein "Nomadentum" in der Welt des Sounds. Solche Klänge, solche Musik führt zu unerwarteten Ergebnissen, so wie auch beim Surfen im Netz, ein solches Stück ist offen, und so wie der Weg beim Surfen immer wieder anders verlaufen kann, es sei denn, ich wähle bewusst den gleichen Weg, so klingt auch diese Musik immer wieder anders, werden die Produktionen jedesmal anders ablaufen, können abgebrochen werden, wie das Surfen im Netz, können auf Irrwege führen - aber man kann auch da an irgendeiner Stelle wieder einsteigen, und dann wird nicht einfach von derselben Stelle aus genau gleich wieder weiter gemacht, sondern von diesem Punkt aus kann der Ablauf ein anderer sein.

Auch wenn das "Material" auf einem Datenträger festgehalten worden ist, jede Vorführung ist neu und vergänglich. Genauso wird es sie nicht mehr geben. Wenn es im Originaltext heißt: "Der User kann sicher sein, immer wieder überwältigend viel an Informationen anzutreffen, aber niemals sicher sein, die Angebote unverändert wieder so anzutreffen, wie er sie schon einmal gesehen hat", so trifft das auf unsere Vorführungen zu, wir müssen nur den "User" durch den "Hörer" ersetzen.

Diese unbegrenzten Möglichkeiten, diese Offenheit können faszinierend sein, d.h. sie verzaubern uns oder etwas negativer sie verhexen uns, m. a.W.: sie ziehen uns in ihren Bann. Warum das so ist, wird ebenfalls an einer anderen Stelle gesagt: "Dieser Flüchtigkeit und der bloßen Virtualität der Kommunikationswelten ist der Mensch aufgrund seiner in prähistorischer Zeit erworbenen Grundausstattung nicht ohne weiteres gewachsen, er muß sich des Dauernden vergewissern, um sein Bewußtseinskontinuum von außen her zu stabilisieren. Die "Antiquiertheit des Menschen" (Günther Anders) angesichts des technologischen Fortschritts wird einmal mehr offenbar". Es ist also die Entsprechung zu unserer Gehirnstruktur. Dieser Befund ist sehr interessant, zeigt er doch auf ganz andere Weise das Menschliche der Elektronischen Musik, die diese Prinzipien realisiert.

Doch wird auch auf ein Phänomen hingewiesen, das wir nur bestätigen können: Freiheit zieht uns nicht nur in ihren Bann, indem sie bei uns angenehme Gefühle, Freude - man denkt hier an "Freude schöner Götterfunke" -auslöst, sie bewirkt auch Angst. Dies hängt, wie auch in diesem Artikel dargelegt, damit zusammen, dass der Mensch, als er sich zum homo sapiens entwickelte, Orientierung und Sicherheit benötigte, um überleben zu können. Uns geht es aber in diesem Bereich nicht ums Überleben, wir können in der Welt der elektronischen Klänge die Freiheit nutzen und die "Antiquiertheit des Menschen" wenigstens versuchen zu überwinden.

Quellen:

"Buch und Internet - Perspektiven einer neuen Medienkonkurrenz," Microsoft(r) Encarta Enzyklopädie 2000. (c) 1993-1999 Microsoft Corporation.

 

In der ersten Folge dieser Csound Reihe [ZeM Heft 23] wurde die Installation beschrieben und ein Programm vorgestellt, mit dem auf einfache Art und Weise Csound bedient werden kann. Den Abschluss bildete das erste Projekt - die Erzeugung eines Sinustons. In diesem Artikel wird der Einsatz von Hüllkurven und LFOs (Low Frequency Oscillators) und deren musikalische Wirkung beschrieben. Außerdem gehe ich näher auf Header, Variablen und P-Felder in Csound ein.

1. Die Hüllkurve

instr 1
a1 oscil 10000, 440, 1
out a1
endin

So sah ein Teil unseres Orc-Files aus dem letzten Artikel aus. Es bewirkt die Erzeugung eines Klanges mit einer Amplitude von 10000 und einer Frequenz von 440 Hz. Die Tonlänge und Grundwellenform wird im Sco-File definiert. Wie muß man dieses File verändern, damit sich die Tonhöhe innerhalb eines Klangs verändert? Der Ton soll innerhalb einer Sekunde von 440 Hz auf 880 Hz gleiten.

istr 1 kfrq line 440, 1, 880
a1 oscil 10000, kfrq, 1
out a1
endin

Zur Lösung dieses Problems benötigen wir den Befehl line. line definiert eine Variable, hier kfrq, der das Gleiten von 440 Hz bis 880 Hz innerhalb einer Sekunde zugeordnet wird. Diese Variable ersetzt in der nächsten Zeile die Konstante 440. Natürlich kann man die Lautstärke genauso verändern. Bei mechanischen Instrumenten verändert sich die Lautstärke kontinuierlich. Spielt ein Instrumentalist einen Flötenton, so hört man zunächst das Anblasgeräusch. Die Lautstärke nimmt danach ab, bis ein konstanter Pegel erreicht wird, bei dem der Instrumentalist den Ton hält. Unterbricht der Instrumentalist den Ton, so folgt eine Ausklingphase. 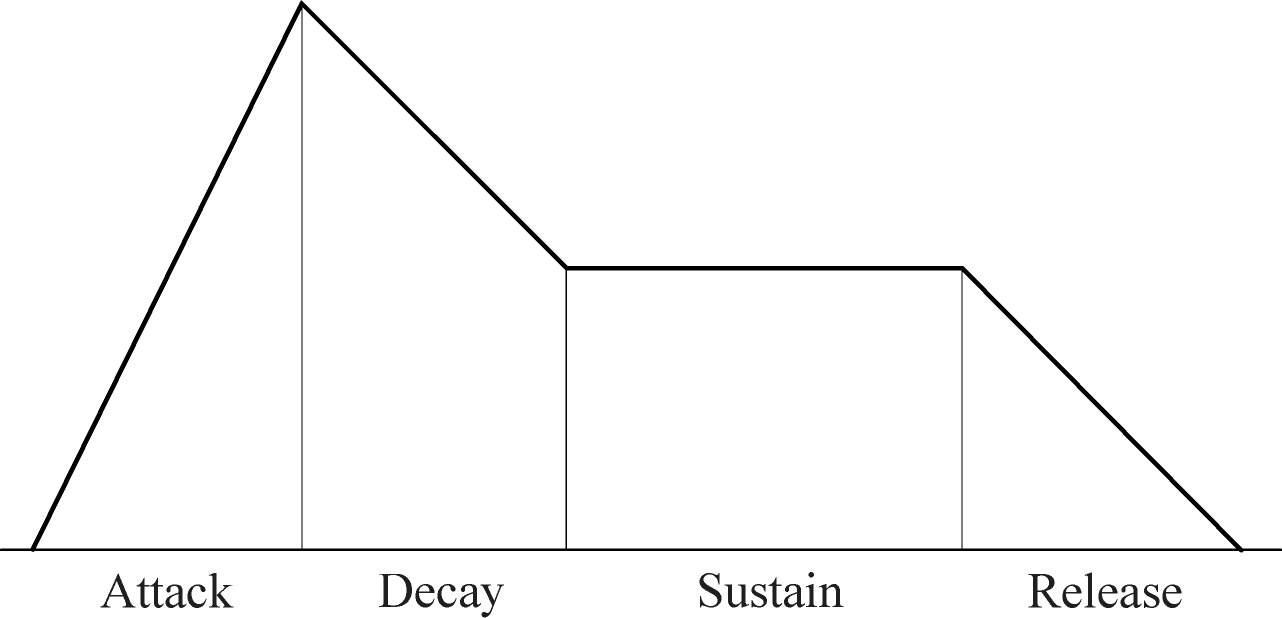Diese "Umschreibung" der Lautstärke wird in Synthesizern von einer Hüllkurve (Envelope) übernommen. Die klassische Hüllkurve wird in 4 zeitliche Phasen eingeteilt:

• Attack: der Ton schwingt ein bis er die höchste Lautstärke erreicht
• Decay: der Ton wird leiser bis er die vom Instrumentalisten gehaltene Lautstärke erreicht
• Sustain: die Haltephase mit konstantem Pegel
• Release: die Ausklingphase, die Zeit zwischen Absetzen und Verklingen des Tons

Diese Phasen werden durch die unten stehende Abbildung verdeutlicht.

Will man unseren Sinuston mit einer Lautstärkenhüllkurve versehen, benutzt man am besten den Befehl linseg.

instr 1
kamp linseg 0, 0.1, 15000, 0.2, 10000, 0.6, 10000, 0.1, 0
kfrq line 440, 1, 880
a1 oscil kamp, kfrq, 1
out 1
endin

Unser Sinuston wurde im oberen Beispiel durch eine Lautstärkenhüllkurve erweitert. Innerhalb 0.1 Sekunden erreicht der Sinus seine höchste Lautstärke von 15000, schwingt innerhalb von 0.2 Sekunden auf 10000 zurück und wird für 0.6 Sekunden auf dieser Lautstärke gehalten. Danach verklingt der Sinus innerhalb von 0.1 Sekunden.

2. Die P-Felder

Meistens will man für unterschiedliche Töne unterschiedliche Frequenzen, Tonlängen oder Lautstärken verwenden. Der erste Ton soll z. B. innerhalb einer Sekunde von 440 Hz auf 880 Hz gleiten. Der zweite Ton soll innerhalb einer halben Sekunde von 880 Hz auf 660 Hz gleiten, usw. Es wäre umständlich, wenn man für jeden Ton ein neues Instrument definieren müsste. Deshalb kann man innerhalb des Orc-Files Variablen definieren, deren Werte erst im Sco-File gesetzt werden. Ein Beispiel haben wir bei unserem Sinus schon kennengelernt. Im Sco-File wird die Tonlänge angegeben. Die ersten drei Parameter des Sco- Files sind festgelegt. Der erste Parameter gibt die Nummer des zu verwendenden Instruments an, der zweite die Startzeit, der dritte die Tonlänge. Weitere Parameterfelder (P-Felder) können im Orc-File definiert werden:

instr 2
ifrq1 = p4
ifrq2 = p5
kamp linseg 0, 0.1, 15000, 0.2, 10000, 0.6, 10000, 0.1, 0
kfrq line ifrq1, 1, ifrq2
a1 oscil kamp, kfrq, 1
out a1
endin

Hier werden zwei P-Felder definiert. Da die ersten drei P-Felder fest vorgegeben sind, beginnt die Definition bei P-Feld 4, hier p4. p4 gibt die Anfangsfrequenz an und p5 die Endfrequenz. Will man das oben beschriebene Szenario programmieren, dann sieht unser Sco-File in etwa so aus:

; instr sta dur frq1 frq2
i2      0   1   440  880
i2      1   .5  880  660
e

Der erste Ton hat eine Tonlänge (dur = duration) von einer Sekunde, beginnt bei einer Frequenz von 440Hz und endet bei 880Hz. Der zweite Ton beginnt nach einer Sekunde und dauert 0.5 Sekunden. Die Frequenz gleitet von 880Hz auf 660Hz. Die 4. Spalte gibt also die Parameter für p4, die 5.Spalte die Parameter für p5 an, usw. Kompiliert man die Files wird die Hüllkurve für den 2.Ton nach einer halben Sekunde abgeschnitten. Ebenso kann das Gleiten von 880Hz auf 660Hz nicht vollständig durchgeführt werden, da im Orc-File 1 Sekunde dafür vorgesehen wurde. Wir müssen das Orc-File derart ändern, dass die Hüllkurve und das Gleiten sich nach der Tonlänge richten. Die Tonlänge wird im Sco-File als 3. Parameter (p3) definiert. Wir müssen also nur statt einer Sekunde eine Variable, die p3 repräsentiert, einsetzen.

instr 2
idur = p3
ifrq1 = p4
ifrq2 = p5
kamp linseg 0, idur*0.1, 15000, idur*0.2, 10000, idur*0.6, 10000, idur*0.1, 0
kfrq line ifrq1, idur, ifrq2
a1 oscil kamp, kfrq, 1
out a1
endin

Den Hüllkurvenlängen werden passende prozentuale Längen zugewiesen. Zusammengerechnet ergibt sich die gesamte Tonlänge: idur*0.1+idur*0.2+iddur*0.6+idur*0.1=idur.

3. Der LFO

LFO bedeutet Low Frequency Oscillator, also niederfrequenter Oszillator. Darunter versteht man in der Regel einen Oszillator der im unhörbaren Frequenzbereich von 0 Hz bis 20 Hz schwingt. LFOs werden für kontinuierlich sich ändernde Klangparameter eingesetzt, z. B. für ein Tremolo oder Vibrato. Ein Tremolo ist ein schneller, kontinuierlicher Wechsel der Lautstärke. Das Vibrato ist der schnelle kontinuierliche Wechsel der Tonhöhe.
In Csound verwendet man für LFOs den oscil Befehl und weist eine entsprechend niedrige Frequenz zu. Das unten stehende Blockdiagramm veranschaulicht den Signalfluss bei einem Tremolo.

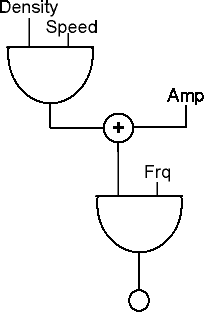
Der Amplitude wird der Wert des LFOs hinzuaddiert. Verwendet man als Grundwellenform des LFOs einen Sinus, wird die sich durch die Addition ergebende Lautstärke kontinuierlich lauter und leiser. Wie oft dieser Wechsel zwischen Laut und Leise auftritt wird durch die Frequenz des LFOs bestimmt. Bei 1 Hz haben wir einen Zyklus pro Sekunde, bei 2 Hz zwei Zyklen, usw. Wie stark der LFO die Lautstärke des Oszillators beeinflusst, wird durch die Amplitude ("Density") des LFOs bestimmt. Je höher die LFO Amplitude, um so größer wird der Unterschied zwischen Laut und Leise. Es folgt das passende Orc-File:

instr 3
idens1 = p4
ispeed1 = p5
alfo1 oscil idens1, ispeed1, 1
a1 oscil 10000+alfo1, 440, 1
out a1
endin

Die LFO Intensität und Geschwindigkeit wird im Sco-File angegeben. Ähnlich verhält es sich, wenn man ein Vibrato erzeugen möchte:

instr 3
idens1 = p4
ispeed1 = p5
idens1 = p6
ispeed1 = p7
alfo1 oscil idens1, ispeed1, 1
alfo2 oscil idens2, ispeed2, 1
a1 oscil 10000+alfo1, 440+alfo2, 1
out a1
endin

4. Header im Orc-File und Grundwellenform im Sco-File

Keines der in diesem Artikel veröffentlichten Listings läßt sich so, wie es aufgeschrieben wurde, kompilieren. Jedes Orc-File muss mit einem Header beginnen. Dort wird die Samplingrate, Kontrollrate und Anzahl der Kanäle angegeben. Diese Header sind hier immer gleich aufgebaut. ksmps ist immer das Ergebnis der Division von sr/kr:

sr = 44100 ; samplingrate
kr = 4410 ; kontrollrate
ksmps = 10
nchnls = 1 ; kanalanzahl

In jedem Sco-File muß zu Anfang die Grundwellenform für die Oszillatoren definiert werden. Dies geschieht mit dem Befehl f. f steht für Funktionstabelle (functiontable). Es wird dabei eine Tabelle definiert, in der die Werte eine Grundwellenform angeben. Eine Sinusdefinition kann folgendermaßen aussehen:

f1 0 8192 10 1

Versuchen sie einmal eine andere Grundwelle, z. B. einen Sägezahn:

f1 0 8192 7 1 8192 -1

5. Ein vollständiges Listing

Zum Abschluss dieses 2.Artikels als Hilfestellung noch das vollständige Listing des Orc- und Sco-Files mit den LFOs:

; orc file header
sr = 44100 ; samplingrate
kr = 4410 ; kontrollrate
ksmps = 10
nchnls = 1 ; kanalanzahl
; body
instr 3
idens1 = p4
ispeed1 = p5
idens2 = p6
ispeed2 = p7
alfo1 oscil idens1, ispeed1, 1
alfo2 oscil idens2, ispeed2, 1
a1 oscil 10000+alfo1, 440+alfo2, 1
out a1
endin

; sco file , funktiontable
f1 0 8192 10 1
; score
; inst sta dur dens1 speed1 dens2 speed2
i3     0   1   500   1      5     2
i3     2   1   10000 2      110   10
e

Vielleicht hat ihnen der Artikel Lust auf mehr gemacht. Dann versuchen sie doch folgende Aufgaben zu lösen:

• wie kann man ein Instrument erzeugen, dass eine Lautstärkenhüllkurve mit von der Tondauer unabhängigen Hüllkurvenphasen hat?
• was passiert, wenn ich den Ausgang des LFOs nicht addiere, sondern subtrahiere, multipliziere oder dividiere?
• was passiert, wenn ich die Frequenz des LFOs erhöhe und so in den hörbaren Bereich komme?
• wie gestalte ich ein Instrument, daß eine Hüllkurve zur Steuerung der LFO Frequenz verwendet?
• wie gestalte ich ein Instrument, in dem ich mehrere Grundwellen gleichzeitig verwenden will?

 

Am 25. Oktober 2001 fand eine weitere Veranstaltung aus der Reihe vorEcho vom Institut für neue Musik an der Staatlichen Hochschule für Musik in Freiburg statt, diesmal unter der Gesamtleitung von Ludger Brümmer. Am Vor - und Nachmittag gab es Vorträge (Claude Cadoz: "Sound Synthesis and Composition with Genesis", Annie Luciani: "Towards Dynamic Visual Arts with Mimesis", Ludger Brümmer: "Musikalische Organismen, Newtonsche Mechanik als kompositorisches Mittel"), diese behandelten ein Programmpaket der ACROE (Association pour la Création et la Recherche sur les Outils d'Expression), das Physical Modelling, Klangsequenzierung und dazu passende Bilderzeugung erlaubt. Siehe dazu auch:
http://acroe.imag.fr/
http://acroe.imag.fr/version-anglaise/sommairecons.html

Am Abend fand ab 20.00 Uhr ein zu den Vorträgen geradezu illustratives Konzert statt. Mesias Maiguashca brachte sein Tonband-Werk "Tiefen" für acht Lautsprecher, ca. 20 min., wie immer bei Maiguashca als reine Musik im Dunkeln abgespielt. Die grundlegende Idee war dabei die Anregung einer Metallplatte, z. B. mit einem Geigenbogen, was mit den o. g. Methoden des Physical Modelling umgesetzt wurde. Bei solchen Resonanzerscheinungen ist es nun so, daß ohne starke Parameterveränderungen der Klang in der wesentlichen Charakteristik gleich bleibt, egal wie stark der virtuelle Bogen oder Klöppel arbeitet, so daß meiner Meinung nach die klangliche Variabilität für ein Werk solcher Dauer etwas gering war. Ich frage mich, ob da nicht mehr zu machen wäre.

Abweichend vom Programm kam dann Hans Peter Stubbes Rhizome, ca. 15 min., für Harfe (Eva Reidel) und Tonband, wobei der Tonbandpart von den Simulationen gezupfter Saiten hergeleitet war. Die Harfenistin befand sich dabei - wie üblich - auf der Bühne des Saales, ihr wurde per Kopfhörer ein Metronom- Pieper zugespielt, damit überhaupt eine zeitliche Orientierung zum Tonband möglich war, das Piepen war übrigens von meiner Position aus die ganze Zeit gut hörbar und etwas störend. Die Problematik der Elektroakustischen Musik trat dabei zu Tage, der menschliche Mitspieler wird von der Elektronik dominiert, quasi ein Sklave des Tonbandes, es ist sicherlich unmenschlich anstrengend, diese Musik einzustudieren und aufzuführen. Ich halte dagegen die Gelassenheit des Komponisten der Elektronischen Musik, der - wie zuvor Maiguashca - einfach sein Band einlegt und startet, er hat alle Arbeit in Ruhe geleistet, wie ein Maler, der sein Bild nach Fixierung und Trocknung in Ruhe betrachtet. Letztere Haltung erscheint mir wesentlich angenehmer und menschlicher. Soweit zur Unmenschlichkeit der Elektronischen Musik.

Ich bin mir nicht sicher, ob es eine gute Idee war, der Harfe synthetische Saitenklänge gegenüberzustellen, vielleicht hätte ein stärkerer Kontrast zwischen Holz und Elektronen mehr gebracht, jedenfalls die genannten Probleme nach dem Motto "entscheidend ist, was hinterher herauskommt" überdeckt. Leider gab es auch einige technische Probleme in Form von Kratzgeräuschen aus den Lautsprechern.

Nach einer Umbaupause kam als Audio/Video-Darbietung "NochDreiSekundenSchwarz" von Hans Tutschku (Musik) und Kerstin Wagner (Video, Darstellerin Yvonne Lachmann), ca. 10 min. Mit dem o. g. Programmpaket wurde Audio und Video erzeugt, wobei die wesentlichen Videoelemente (Arme, Mund und Auge) eine wirbelnde Choreographie auf der Leinwand vollführten, wobei einige Sequenzen in mir Assoziationen zu "Un chien andalou" von Salvador Dalí und Luis Buñuel (1929), erweckten, natürlich in Farbe und mit den heutigen Möglichkeiten. Eine surreale Entsprechung von Video und Audio, einfach schön.

Den Abschluß bildete Ludger Brümers "Medusa", für zwei Schlagzeuger (Ricardo Marini, Pascal Pons) und Vier-Kanal-Tonband und Video, ca. 28 min. Auch hier mußte dem Menschen eine akustische Hilfe per Knopf im Ohr zur Orientierung gegeben werden, es gilt auch das Problem der Unmenschlichkeit. Links und rechts von der Leinwand agierten die Schlagzeuger mit Cymbals, Gong, Xylophon usw., während sich auf der Leinwand geometrisch abstrakte Strukturen bildeten, sich veränderten und verschwanden. Ganz früher, als vormittags noch kein Infotainment aus dem Fernseher quoll, als es nur drei Programme Volksfernsehen gab, konnte man einen sehr primitiven Vorläufer dieser Strukturen als Pausenzeichen des WDR sehen, in ihrer fächerförmigen Gestalt einem Hauptmotiv in der Videoproduktion entfernt verwandt. Auch hier fehlte es mir etwas an Kontrast zwischen Schlagzeug und Tonband, das ist vielleicht wieder mein persönliches Problem.

Ich weiß, es ist ungerecht und absolut ungerechtfertigt, aber diese Produktion hatte etwas, sie machte einen kompakten Eindruck, man hatte das Gefühl "das paßt", diese farbigen, synthetischen Strukturen, immer etwas im Nebel, unscharf, abstrakt, bedeutungslos, nicht zu interpretieren, und dazu die Musik. Für mich der Gewinner des Abends. Wäre der Schlagzeugpart auch vom Band gekommen, so hätte mich dies keineswegs gestört, noch das Ergebnis wesentlich verändert, z. T. war es sowieso schwer auszumachen, woher der Klang nun eigentlich kam.

Leider gibt es in dem großen Saal der Musikhochschule ein Problem mit Resonanzen, irgendwelche Strukturen der Einrichtung, oder vielleicht sogar die Parkettleisten lassen sich bei tiefen Tönen zu schnarrenden Resonanzen anregen.

Man kann es nur immer wieder betonen: ca. 40 Leute im Publikum ist kein Ruhmesblatt für eine Universitätsstadt wie Freiburg mit immerhin gut 200.000 Einwohnern und für die Musikhochschule im Besonderen. Es fanden an diesem Tag auch Prüfungen statt, die sicher irgendwie auch unmenschlich sind, somit hatten einige Studenten und Professoren sicherlich anderes zu tun. 12 DM Eintritt (ermäßigt sogar nur 6 DM) sind auch kein Argument, fernzubleiben. Alle Akteure hätten mehr Interesse verdient, keine Frage. Gerade deshalb muß man dankbar sein, daß eine Reihe wie vorEcho weiter besteht, Elektronische oder "elektroakustische" Musik wäre sonst in Freiburg kaum zu hören.

 

Mathematik und Musik sind für die meisten Leute gegensätzlich, ja unvereinbar. So ist es für manche bisweilen eine schockierende Erfahrung, daß es schon im Altertum im nichttrivialen Quadrivium der sieben freien Künste (Arithmetik, Astronomie, Geometrie, Musik) Tonkunst und Mathematik in schönster Eintracht neben- und miteinander gab, sich gegenseitig befruchtend. In der Elektronischen Musik nun gewinnt die Mathematik sehr stark an Bedeutung, sei es in der Komposition (Aleatorik, Serialismus), oder in der Signalverarbeitung. Gerade im letzteren Bereich sind die Möglichkeiten in den letzten Jahren durch die Digitaltechnik - und das ist endliches Zahlenrechnen mit höchster Geschwindigkeit - so enorm gewachsen, daß erfolgreiches Produzieren ohne Grundlagenkenntnisse der beteiligten mathematischen Prozesse mir immer mühsamer und aussichtsloser erscheint. Durch Versuch und Irrtum wird man nicht sehr weit kommen, ja man kann künstlerisch auf der Stelle treten, die Frustrationsgefahr wächst. Mathematische Einsichten können da helfen. David Hilbert hat das einmal so formuliert: "Die Mathematik ist das Instrument, welches die Vermittlung bewirkt zwischen Theorie und Praxis, zwischen Denken und Beobachten: sie baut die verbindende Brücke und gestaltet sie immer tragfähiger. Daher kommt es, daß unsere ganze gegenwärtige Kultur, soweit sie auf der geistigen Durchdringung und Dienstbarmachung der Natur beruht, ihre Grundlage in der Mathematik findet". Die Beschäftigung mit der Mathematik ist daher äußerst lohnend für den Produzenten Elektronischer Musik, aber was sind die Kosten? Ich versuche hier auf wenigen Seiten einen Vorgeschmack zu geben. Jeder mag das Opfer dann selbst einschätzen. Über einige geschichtliche Anmerkungen komme ich zu wichtigen Grundvoraussetzungen, die dann erlauben, nichtlineare dynamische Systeme zu untersuchen und zu beschreiben, und das sind die Systeme, um die es bei Elektronischer Musik vor allem geht.

Denkweise und Geschichte

Für mich ist die Mathematik eine reine Geisteswissenschaft, denn sie behandelt rein geistig abstrakte Konstruktionen und deren Beziehungen untereinander. Denn es gibt in der Natur keine Kreise, keine Zahlen, keine Matrizen, keine Vektoren, keine Mengen.

Im geschichtlichen Ablauf war dies nicht immer so deutlich, da die Entwicklung von Mathematik und Physik Hand in Hand vonstatten ging, oft in Personalunion z. B. eines Isaac Newton, nach den jeweiligen praktischen Erfordernissen. Dadurch gab es ein gewisses Durcheinander, das dann in einem Revisionsprozeß im 19. und 20. Jahrhundert bereinigt wurde, um die gesamte Mathematik auf ein solides, geordnetes und logisches Fundament zu stellen. Um diese Zeit gab es schon wichtige Ergebnisse, die keinerlei praktische Anwendung hatten, also reine Mathematik, und es ist seitdem immer mehr geworden. Wie in jeder anderen Disziplin findet eine Aufspaltung in verästelte Gebiete statt, in denen sich nur eine kleine Zahl von Experten auf der ganzen Welt auskennt.

Ich muß den Leser also zunächst enttäuschen, in der Schule haben wir nur etwas Arithmetik, etwas Geometrie, etwas elementare Algebra und wenn es gut ging auch etwas Analysis gelernt, aber das ist nicht Mathematik, sondern das sind nur wichtige Teilergebnisse der klassischen Mathematik vor nunmehr fast 300 Jahren. Alles was danach kam ist meist deutlich schwieriger und den praktischen Anforderungen meist weiter entrückt. Das hat natürlich auch Vorteile: wenn die für uns praktisch wichtige Mathematik so alt ist, so wird sie allgemein gut verstanden sein, werden die Ergebnisse solide und abgesichert sein und es wird eine entwickelte Didaktik geben.

"Ein Grund für die spezielle Wertschätzung der Mathematik über alle anderen Wissenschaften hinaus ist, daß ihre Gesetze absolut sicher und unanzweifelbar sind, während die der anderen Wissenschaften immer zu einem gewissen Grad unsicher sind und zudem in stetiger Gefahr sich befinden, von neuen Tatsachen komplett entwertet zu werden" (Albert Einstein). Hier tritt eine einzigartige Eigenschaft der Mathematik zu Tage. Was sind physikalische, medizinische, chemische, musikalische, astronomische oder archäologische Theorien von vor 300 Jahren heute noch wert? Wenig oder meist nichts! Der Satz des Pythagoras ist nun ca. 2500 Jahre alt, aber er besteht immer noch, und daran wird sich auch nichts ändern. Die alten Griechen haben nämlich den öffentlichen Beweis in die Mathematik eingeführt, und zwar in wesentlich strengerer Form als den "Beweis" vor Gericht.

Es gibt gewisse vernünftige Grundannahmen (Axiome) über die man sich verständigt, ebenso über die Regeln des richtigen Schließens (Logik). Ab diesem Punkt kann ein mathematischer Beweis von allen Fachleuten Schritt für Schritt kritisch diskutiert und nachvollzogen werden, jedes Glied der Beweiskette muß dabei standhalten, sonst fällt alles in sich zusammen. Dies ist eine totale Abkehr von der religiösen Geheimwissenschaft der ägyptischen und babylonischen Mathematik-Priester-Praktiker, die zwar Rezepte hatten, aber meist nicht wußten, warum sie funktionierten [1]. "Ich meine das Wort Beweis nicht im Sinne der Juristen, die zwei halbe Beweise einem ganzen gleichsetzen, sondern im Sinne der Mathematiker, wo ein halber Beweis nichts ist und wo für einen Beweis verlangt wird, daß jeder Zweifel unmöglich ist" (Carl Friedrich Gauß).

Seither sind Axiome die Grundlage eines mathematischen Bereiches, darauf gründen sich per strengem Beweis die Sätze (Theoreme, also bewiesenermaßen wahre Aussagen), und Hilfsätze. Über allem thront die mathematische Logik, die festlegt, was eigentlich ein Beweis ist. Es gibt zwar auch Vermutungen, diese sind aber nur Ansporn, den Beweis für die Richtigkeit der Vermutung zu führen, die Suche mag Jahrhunderte dauern, niemand wird jedoch in der Mathematik etwas auf Vermutungen aufbauen.

Deshalb gibt es in der Mathematik eigentlich nur Evolution, keine Revolution. Tausende Jahre alte Ergebnisse sind und bleiben gültig. Freilich hat diese ungebrochene Tradition insofern ihre Nachteile, als daß es implizite Festlegungen gibt, die die Insider gar nicht mehr als solche erkennen. Das Symbol für die Zahl Pi ist noch jedem bekannt, aber e als Basis des natürlichen Logarithmus, x, y und z für die drei kartesischen Raumkoordinaten, allgemein x für die unabhängige Variable, a, b und c für Parameter, die ganzen Operatoren und sonstigen Symbole, sie sind alle fast 300 oder gar mehr Jahre alt.

Euklid war ein guter Lehrer, er hat sein Geometriewerk "Die Elemente" vor 2300 Jahren lehrbuchmäßig in Strenge entwickelt, und so wird im wesentlichen heute noch gelehrt. Dazu stellte er zunächst vier Axiome auf:

• Zwischen zwei Punkten kann eine Strecke gezeichnet werden.
• Jede Strecke kann unendlich verlängert werden (man hat also eine Gerade).
• Für jede Strecke gibt es einen Kreis mit der Strecke als Radius und einem Endpunkt der Strecke als Mittelpunkt des Kreises.
• Alle rechten Winkel sind deckungsgleich (kongruent).

Und dazu ein fünftes Axiom:

• wenn man eine Gerade zeichnet und einen Punkt, der nicht auf der Geraden liegt, so gibt es genau eine Gerade, nämlich die Parallele, die durch diesen Punkt geht, und die Ausgangsgerade nie schneidet.

Hier sieht man schön die geistige Abstraktion: es gibt keine materiellen Punkte und Geraden, weder mit Schnur und Kreide noch mit Tinte. Ja, es gibt noch nicht einmal die perfekte Ebene, die Euklid voraussetzte. Sie sehen an diesem Beispiel auch, wie fundamental Axiome sind. Im genannten Revisionsprozeß hat man die Sache noch einmal ganz genau geprüft und festgestellt: Euklid hatte einige zusätzliche Grundannahmen - die ihm völlig evident erschienen - gar nicht erst erwähnt. Aus der modernen Sicht - 2300 Jahre später - hat die Erfahrung die Mathematiker dazu bewogen, diese Lücken zu stopfen, die Euklidische Geometrie z. B. nach Hilbert hat demnach 20 Axiome, was am Endergebnis jedoch gar nichts ändert, denn Euklid hatte die richtigen Schwerpunkte gesetzt, die Mängel waren also eher formaler Natur.

Das fünfte Axiom ist nun merkwürdig, es erscheint weniger zwingend als seine vier Vorgänger. Daher versuchte man lange, die Aussage des fünften Axioms aus den vier anderen heraus zu beweisen, was aber unmöglich ist. Was kann man sonst tun? Was passiert, wenn man am fünften Axiom des Euklid ändert? Solch frevelhaftes Denken war erst lange nach der Aufklärung im 19. Jahrhundert möglich und man kam zu zwei weiteren vollgültigen Geometrien: eine mit unendlich vielen Parallelen, und eine andere ohne jegliche Parallele im euklidischen Sinn.

Wir haben also im Bereich der Geometrie drei unterschiedliche Theorien, die sich durch das fünfte Axiom unterscheiden, jede mit eigenen Lehrsätzen und untereinander unvereinbaren Aussagen, jede ist für sich logisch und widerspruchsfrei. Welche ist nun "die Richtige"? Diese Frage läßt sich innerhalb der Mathematik nicht beantworten. Man kann sich aber fragen, welche für die Physik am geeignetsten erscheint. Die Erde ist beinahe eine Kugel, Euklids Geometrie der Ebene stimmt also hier bei langen Strecken nicht, z. B. bei der Planung von Flugrouten.

Damit kommen wir zu einem ganz wichtigen Punkt, dem der Interpretation. Innerhalb der Mathematik hantieren wir nach bestimmten Regeln mit Symbolen, z. B. Ziffern in der Arithmetik. Ob eine Operation korrekt ist, oder nicht, läßt sich leicht entscheiden. Dann aber kommt die Interpretation des Ergebnisses. Nehmen wir ein einfaches Beispiel: 5 + 4 = 8. Wenn wir "=" als "gleich" interpretieren, so ist die Aussage falsch. Wenn wir es aber als "größer oder gleich" interpretieren, so ist die Aussage richtig. Wir müssen also über eine widerspruchsfreie Interpretation unseres Formalismus verfügen. D. h.: wir müssen eine praktische, z. B. physikalische Fragestellung zuerst in einen geeigneten mathematischen Formalismus abbilden, sozusagen die richtige Mathematik dafür aussuchen, dann lassen wir den Formalismus ablaufen, das Ergebnis jedoch müssen wir jedoch wieder außermathematisch interpretieren. Wenn der gewählte Formalismus nicht paßt, werden wir keine sinnvolle Interpretation der Ergebnisse finden können und umgekehrt. "Wie kann es sein, daß die Mathematik als Produkt reinen menschlichen Denkens, und somit unabhängig von der Erfahrung, so bewundernswert zu den Objekten der Realität paßt?" (Albert Einstein).

In der Schule wird viel Zeit mit Rechnerei verbracht, außerdem werden die Ebenen der Abbildung, des Formalismus und der Interpretation ständig unreflektiert vermischt, infolgedessen scheitern die meisten bei der Abbildung oder bei der Interpretation. Formales Rechnen ist Fleißarbeit, man kann es durch Fleiß zu etwas bringen. Die beiden anderen Bereiche erfordern jedoch Einsicht, Fleiß genügt hier nicht. Dies mag für viele die wesentliche Hürde beim Lernen gewesen sein.

Das solchermaßen errichtete Gebäude der Mathematik sieht recht solide aus, aber gibt es auch vielleicht versteckte Risse? Ja, die gibt es. Genau wie die Physik 1927 mit Heisenbergs Unschärferelation an eine fundamentale Grenze stieß, so geschah es in der Mathematik, als Gödel 1932 seinen Unvollständigkeitssatz bewies. Dieser besagt, daß jedes mathematische System mit seinen Axiomen, Sätzen, Beweisen und Interpretationen entweder unvollständig ist, also nicht alle möglichen Wahrheiten beinhaltet, oder aber in sich selbst widersprüchlich ist. 1932 war dies ein Schock, heute hat man sich an limitative Ergebnisse dieser Art in den Wissenschaften schon längst gewöhnt [2].

Das Vorausgegangene war ein Versuch, unter den Schuttbergen aus Hausaufgaben, Auswendiglernen, Rechenschiebern, Tabellenwerken und zweifelhaften Lehrbüchern das Wesen der Mathematik noch einmal auszugraben. Ich möchte nun an konkreten Beispielen einige wichtige Ergebnisse und Methoden kurz ansprechen, die für die Elektronische Musik von äußerster Wichtigkeit und von größtem Nutzen sind, dabei wird auch eine Vermischung der drei Ebenen Abbildung, Formalismus und Interpretation stattfinden.

Komplexe Zahlen

Im folgenden werden wir in der Praxis sehen, daß es nützliche und interessante mathematische Bereiche außerhalb der üblichen Schulbildung gibt. In der Schule vollziehen wir ja gleichsam die Menschheitsgeschichte am Individuum nach, wir starten mit den Natürlichen Zahlen 1, 2, 3, 4, ..., die sicher schon vor 6000 Jahren gedanklich entwickelt waren, wie z. B. Zahlenschnüre beweisen. Hinzu kommt dann die Zahl 0, dann Negative Zahlen und somit die Ganzen Zahlen ... , -3, -2, -2, 0, 1, 2, 3, ..., dazu dann die Brüche, also haben wir die Rationalen Zahlen.

Schon um 2500 v. u. Z. kannte man die Irrationalen Zahlen, wie z. B. die Quadratwurzel aus 2 und die Transzendenten Zahlen wie Pi. Die gesamte Menge all dieser genannten Zahlen bildet die Menge der Reellen Zahlen, so genannt, weil sie "dicht genug" beieinanderliegen um jeglichen Meßwert und jedes Rechenergebnis aus der realen Wert auszudrücken. Aber die Reellen Zahlen reichen nicht, denn wenn Sie in der Schule eine Aufgabe zu lösen hatten, bei der am Ende die Wurzel aus einer negativen Zahl zu berechnen war, so konnten sie sicher sein, einen Fehler gemacht zu haben. Die Wurzel aus einer negativen Zahl kann man doch nicht ziehen, der Taschenrechner sagt: "ERROR", oder? Nun ist es so, daß schon ganz einfache Gleichungen dadurch recht merkwürdig werden. Betrachten wir das folgende Beispiel:

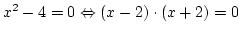
Gesucht ist als die Lösung einer einfachen Quadratischen Gleichung, die gleich äquivalent umgeformt in Produktform daneben steht. Es gibt also offensichtlich zwei Lösungen, 2 und -2. Probieren Sie es aus! Jetzt verändern wir die Gleichung ein klein wenig:

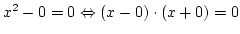
Die Konstante wurde von -4 auf 0 abgeändert, dies ist trivial und ergibt 0 als doppelte Lösung, wie die Produktform zeigt. Nun ändern wir die Konstante auf 1 und es gibt scheinbar überhaupt keine Lösung mehr:

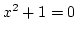
Denn welche Zahl x ergibt mit sich selbst multipliziert -1, also eine negative Zahl und hebt damit die Konstante 1 weg zu Null?

Quadrieren und Quadratwurzelziehen sind zueinander inverse Operationen. Ich kann jede Relle Zahl quadrieren, aber nur aus den positiven Rellen Zahlen die Wurzel ziehen. Dies ist merkwürdig. Und: die Terme auf der linken Gleichungsseite waren Polynome, also Ausdrücke der Form:

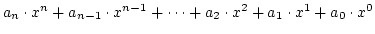
wobei die a_n feste Zahlenwerte sind, die sogenannten Koeffizienten. Polynome sind praktisch sehr wichtig, wir werden dies später noch behandeln. Es ist daher nicht einzusehen, daß solche Nullstellenprobleme mit Polynomen - wie oben gezeigt - manchmal n, manchmal aber gar keine Lösung haben sollen. Offenbar hat die Mathematik hier eine Lücke.

Jetzt kommt eine typisch mathematische Vorgehensweise: man identifiziert genau das Fehlende. Im gezeigten Beispielfall ist es die Quadratwurzel aus -1. Alle anderen Fälle lassen sich darauf zurückführen. Wir wissen, daß diese Wurzel normalerweise nicht existiert, denn welche Zahl ergibt mit sich selbst multipliziert etwas Negatives? Deshalb stopfen wir die Lücke, indem wir genau dies hinzufügen, wir sagen einfach: "Die Wurzel aus -1 existiere, es sei die Zahl i, die imaginäre Einheit". Es gilt damit auch per Definition:

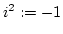
Damit ist die Produktform des letzten Problems:

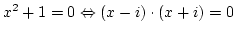
also ist die Lösung -i und i.

Wir kommen somit zu einem erweiterten Zahlenbegriff, dem der Komplexen Zahlen. Eine solche Zahl z setzt sich aus einer gewöhnlichen reellen Zahl a, dem Realteil, sowie einer reellen Zahl b, dem Imaginärteil, mal der imaginären Einheit i wie folgt zusammen:

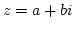
Ist a gleich Null, so ist z rein imaginär. Ist b gleich Null, so ist z rein reell. Alles dazwischen ist komplex. Das Wunderbare an dieser Erweiterung des Zahlenbegriffes ist nun, daß sie konservativ ist, alles bisher Gelernte über Arithmetik und Algebra gilt weiterhin, man muß nur stets die Regeln beachten. Lassen Sie uns das ganze einmal geometrisch in der Ebene des Euklid betrachten. Die natürlichen Zahlen lassen sich auf dem Zahlenstrahl abtragen. Ich erinnere mich noch an meinen ersten Schultag, als ich diesen Zahlenstrahl, das ganze Klassenzimmer umlaufend, erblickte, von 1 bis 10000. Wir wissen, daß es auch negative Zahlen gibt, diese brauchen einen negativen Bereich, also benötigen wir eine Zahlengerade wie in der Abbildung:

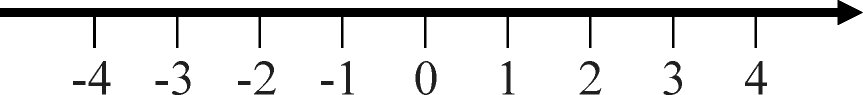
Die Reellen Zahlen, die uns helfen, die Physik abzubilden, sind beliebig "feinkörnig", sie liegen dicht überall auf dem Zahlenstrahl. Die komplexen Zahlen lassen sich nicht mehr auf einer Zahlengeraden unterbringen, sondern sie bedürfen der komplexen Zahlenebene. Die Reelle Zahlengerade ist dort natürlich mit eingeschlossen. Betrachten wir dazu die folgende Abbildung:

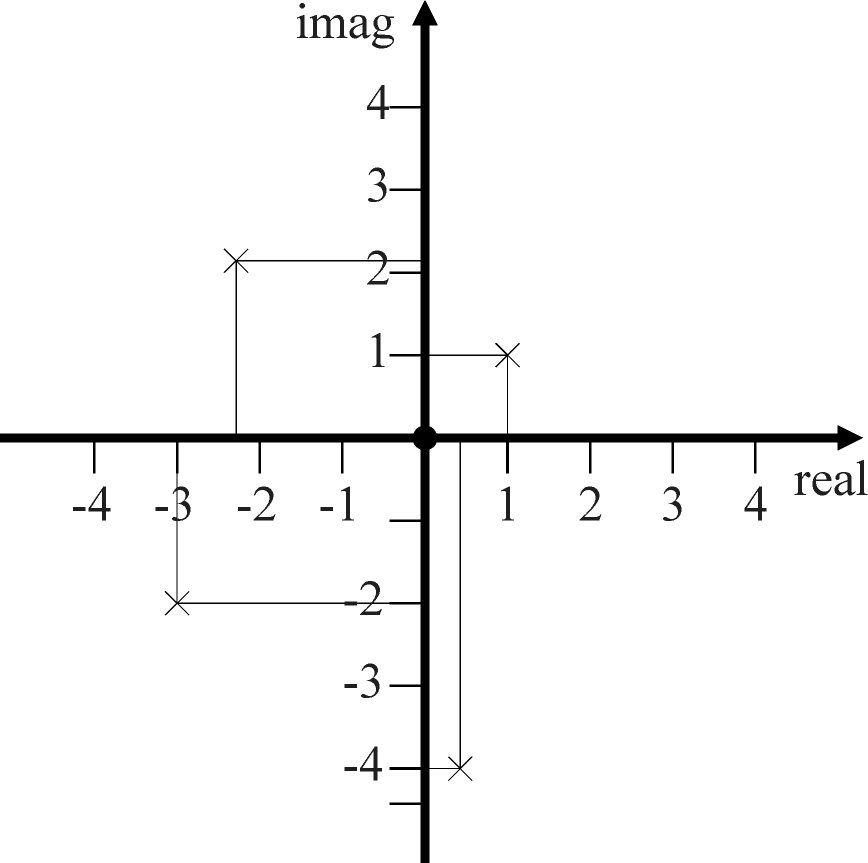
Die rein rellen Zahlen liegen dabei auf der rellen Achse (z. B. -3 oder 2.1). Die rein imaginären Zahlen liegen auf der imaginären Achse (z. B. 2i, -4i). Ich habe vier komplexe Zahlen eingezeichnet, zusammen mit deren Abtragungen auf den Achsen (0.4-4i, 1+1i; -2.2+2.1i; -3-2i). Sie sehen, daß man bei komplexen Zahlen von einer Relation wie "größer" oder "kleiner" nicht mehr sprechen kann, denn es gibt in der Ebene nur links, rechts, oben und unten. Man kann aber den Betrag einer komplexen Zahl angeben, und das ist der Abstand vom Nullpunkt der Zahlenebene, oder nach Pythagoras und den vorher eingeführten Bezeichnungen:

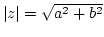
Sie sehen: alles kehrt wieder, nichts ist in der Mathematik verloren. Dies alles wäre jetzt völlig uninteressant, wenn es für unsere Zwecke keine passende Interpretation gäbe. Komplexe Zahlen können jedoch sinusförmige Schwingungen sinnvoll repräsentieren, sie sind unentbehrlich bei der Berechnung von Frequenzgängen, Filtern und der Lösung von Differentialgleichungen. Schließlich kann man mit ihnen die wunderbaren Apfelmänchen der chaotischen Mandelbrot-Menge berechnen, oder die Figuren der Julia-Menge.

Funktionen

Bisher waren die Lösungen einer Gleichung gesucht, und das waren Zahlen, ob nun reell oder komplex, jedenfalls punktuelle Größen ohne Ausdehnung. Die uns interessierenden Größen wie die elektrische Spannung U oder der relative Schalldruck p, oder aber auch eine Melodielinie lassen sich aber in ganz natürlicher Weise als Funktionen der Zeit beschreiben. Man schreibt z. B. p(t). Was bedeutet das? Die Funktion p(t) kann man sich als unendliche Tabelle vorstellen, in der für jeden Zeitpunkt t (die Variable) genau ein Druckwert p(t) (der Funktionswert) eingetragen ist, z. B. durch eine ideale Messung. In der Abbildung habe ich solch eine Tabelle für einige Meßwerte einmal angelegt:

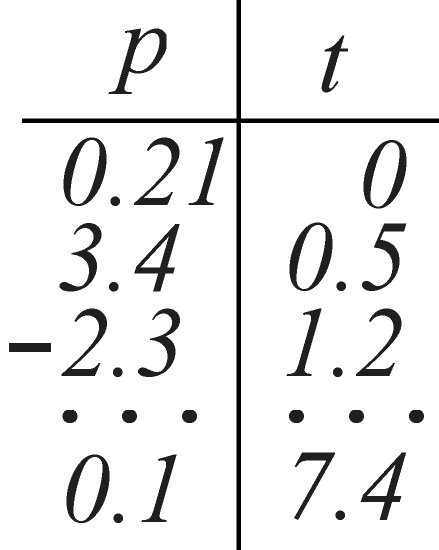
Die Zeit könnte dabei z. B. in Sekunden gemessen werden, der Druck in Pascal. Die Idee, daß für wirklich jeden Zeitpunkt t ein Meßwert eingetragen ist und sei er noch so fein aufgelöst, läßt sich dabei nur schwerlich darstellen. Es ist auch möglich, p(t) für negative Zeiten einzutragen, was üblicherweise die Vergangenheit symbolisieren soll. Es gibt aber auch Funktionen die nur zu ganz bestimmten Variablenwerten (sprich Zeiten) einen Wert aufweisen, Sound- Sampling läßt sich so beschreiben. Zum Schluß kann die Variable nicht nur die Zeit, sondern z. B. den Ort, die Temperatur oder andere physikalische Größen beschreiben.

Anstatt durch eine Tabelle kann man Funktionen einfacher durch eine Rechenvorschrift oder Formel beschreiben, dies ist sogar der übliche Weg. Also:

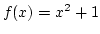
Dies ist die bekanntere Darstellung, f(x) als Funktion der Variablen x. Die Formel besagt nun, daß für jede Zahl x diese zum Quadrat zu nehmen ist und 1 hinzu zu addieren ist, um dann den Funktionswert für diese Zahl x zu erhalten. Die Formel als Rechenvorschrift für alle x beinhaltet somit die unendliche Tabelle in sich, und dies in handlicher Form.

Der dritte, und vielleicht anschaulichste Weg, sich einer Funktion zu nähern ist der Funktionsgraph. Man trägt die Werte der Variablen und die entsprechenden Funktionswerte als Punkte in ein Diagram ein. Sie kennen das Verfahren schon von den Graphen der Börsenkurse her. Für die Beispieltabelle mit vier Werten habe ich dies durchgeführt, vollziehen Sie dies einmal nach:

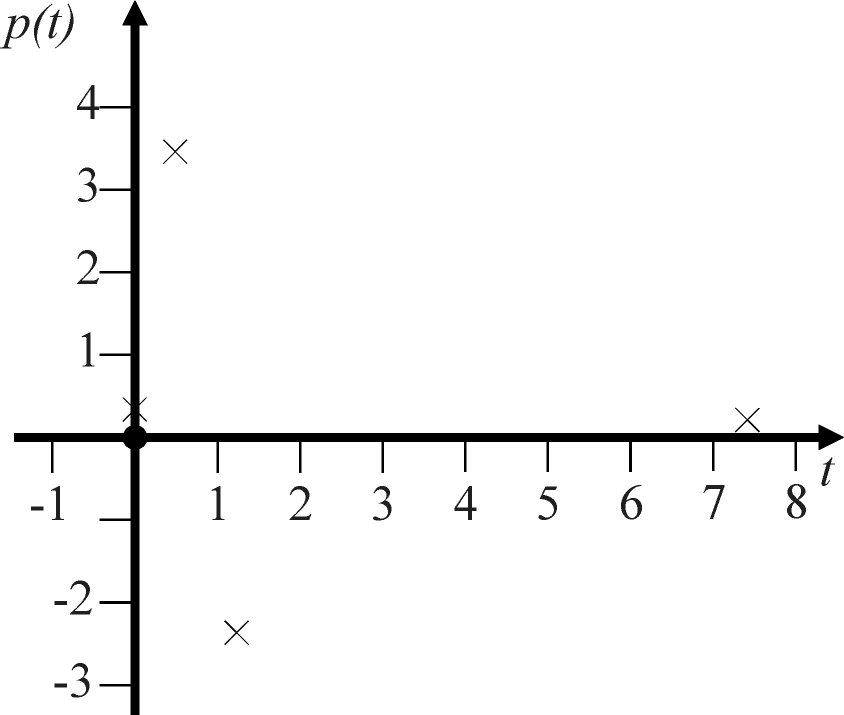
Für mehr Werte wird dies lästig, aber wozu haben wir schließlich Computer? Es gibt ein kostenloses Program namens Gnuplot zur Berechnung der Graphen unter: http://www.gnuplot.info/. Dort findet man auch eine Menge Zusatzprogramme und Tutorials. Das folgende Beispiel für die Funktion (2) habe ich mir von Gnuplot ausrechnen lassen:

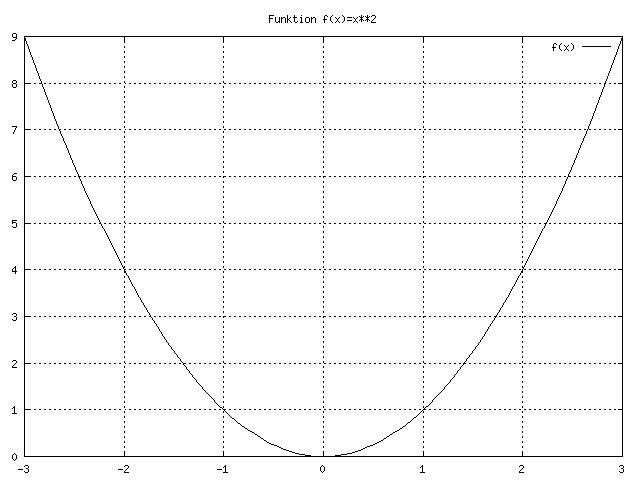
Wie für die Zeichnungen in der Geometrie, so gilt auch für Funktionsgraphen: Man darf ihnen nicht zu sehr trauen und man kann nichts mit ihnen beweisen. Denn wenn wir bei unserem Bild der Funktion ahnungslos "wichtige" Punkte weglassen, oder zu grob auflösen, können wir ein in wesentlichen Eigenschaften falsches Bild der Funktion bekommen. Das physische Bild hilft sehr beim Nachdenken, kann die geistige Analyse aber niemals ersetzen.

Quellen:
[1] Simon Singh : Fermat's Last Theorem : Petersen, Hamburg; Fourth Estate
[2] Douglas Hofstadter : Gödel, Escher, Bach : Ernst Klett Verlag